5 对一艘走私船的二分搜索（第2/2页）

“我们的目标值是19，我们的算法是二分搜索。现在搜索空间是整列船只，所以我们已经有了上界和下界，如果我们使用闭合区间，那么我们的下界是第一艘船，上界是最后一艘船。如果Retry Loop在这里，很明显它不会在第一艘船之前，也不会在最后一艘船之后。

“现在我们从中间的那艘船开始，询问它是何时到港的，如果它的到港时间不足19个小时，那它肯定在Retry Loop之前。这样可以将我们的搜索分为两块，然后……”

“如果它是19个小时以前抵达的，则它一定在Retry Loop之后，”Notation抢在Frank之前说，“我知道二分搜索，我的警用算法课的期末考试就在两个半月之前。”

确定搜索算法后，他们俩就动身去找Retry Loop。中间的船是一艘闻起来有股怪香蕉味的黄色帆船，它是17个小时前抵达的。

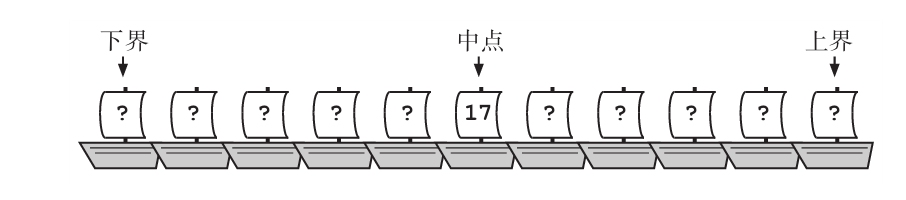
这意味着他们可以排除前面一半的船只了，包括中间这艘。Frank将下界调整为黄色帆船之后的那艘船。

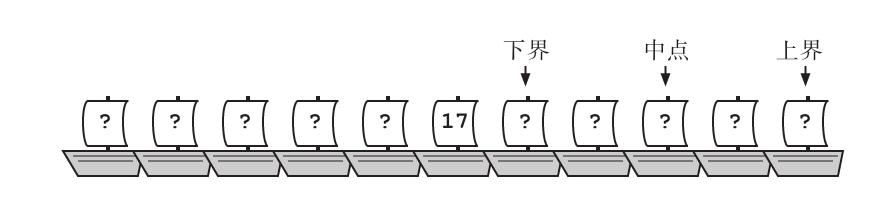
搜索空间缩小后，他们选择了一个新的中点。他们花了好一段时间才让这个船长相信他们不是海关的卧底。十分钟之后，Notation将她的徽章推到了船长的眼前，船长的语气立即变得愤怒而抱怨，他说他的船Corrupt Packet已经被困在这个港口22个小时了，要求他们代表他和海关长谈谈。

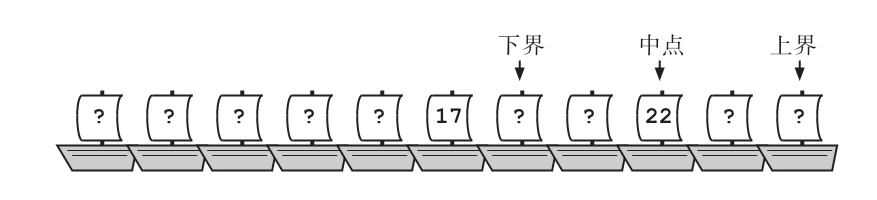
因为目标是19个小时，所以他们知道Retry Loop是在Corrupt Packet之前抵达。他们又一次改变了界限，所以现在Corrupt Packet左边的船是新的上界。

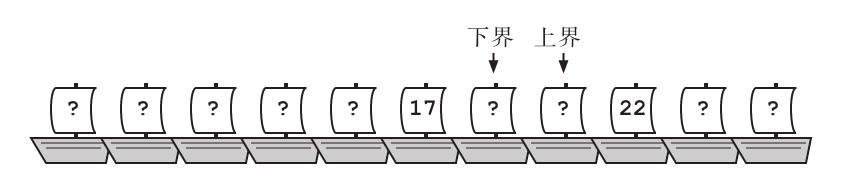
只剩下两艘船在搜索范围内了，搜索即将结束。如果这两艘船都不是Retry Loop，他们就能确定它已经离开了港口，因为一旦搜索空间没有更多的元素，他们就可以排除整个搜索空间。

因为现在只剩下两艘船，他们可以选择其中任意一个作为中点，根据直觉，Frank选择了早些抵达的船，也就是它们中的下界。与一个在码头闲逛的水手进行简单对话后，他们确定这艘船就是Retry Loop，它已经抵达19个小时了。

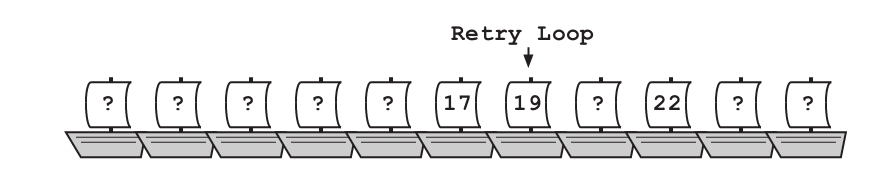
“现在怎么办？”他们看着那艘船，Notation问道。

“我们要用你那枚闪亮的徽章。”Frank回答道。

警用算法导论：二分搜索Ⅰ

节选自Drecker教授讲义

二分搜索算法用于高效地在有序数组A中查找一个目标值v。和线性搜索不同，二分搜索利用数据结构中的信息让搜索更高效。高效算法的关键是信息。在下面的例子中，我们就要使用数组是按照升序排序的这个信息：

对于一对索引i和j，如果i<j，则有A[i]≤a[j]

这看起来并不是很多的信息，但是它足够让我们的搜索更加高效。

二分搜索算法的工作原理是：不断地将搜索空间分成两半，并且把搜索空间限制在其中的一半中。这个算法通过改变上下界限有效地限制了搜索空间。上界（IndexHigh）标记了搜索空间有效数组中最高的索引，下界（IndexLow）标记了搜索空间有效数组中最低的索引。通过这个算法，如果目标值在这个数组中，就可以保证：

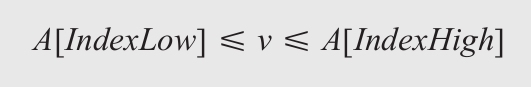
在搜索的每一步中，我们只需依次判定上界和下界中间的值：

接下来，我们将中间值A[IndexMid]和目标值v进行比较。如果中间值小于目标值（A[IndexMid]<v），我们就知道目标值一定介于这个中间值之后。这样我们可以将IndexLow改为IndexMid+1来使搜索空间又变成原来的一半。

如果中间值比目标值大（A[IndexMid]>v），我们就知道目标一定位于中间值之前，于是我们将IndexHigh改为IndexMid-1来使得搜索空间变成原来的一半。

当然，如果我们发现A[IndexMid]等于v，我们可以直接结束搜索，找到目标值。

现在我们就来使用二分搜索在下面这个已排序的数组中寻找到15。虚线框出的方块是算法当前需要判定的值，而被阴影遮住的部分则是在搜索中被排除的部分。

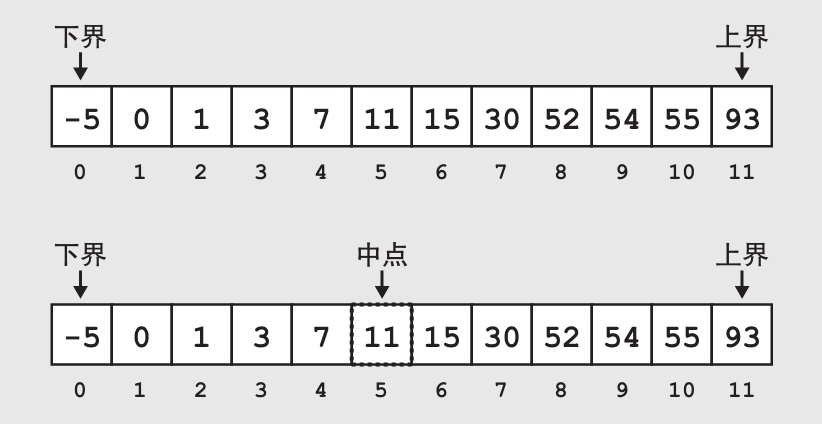
第一个被判定的中点的值是11，比我们的目标值15小。因为我们知道这个数组是按照升序排列的，所以可以排除中点及其之前的所有部分。我们将下界索引移动到适当的地方（IndexLow=IndexMid+1）。

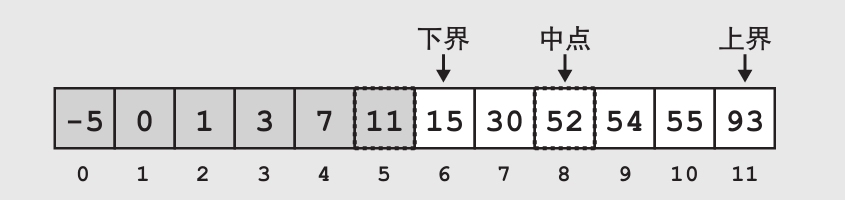
在第二次比较之后，我们发现中点值是52，比目标值大。我们可以排除中点和它之后的所有部分。此时需要移动我们上界（IndexHigh=IndexMid-1）。

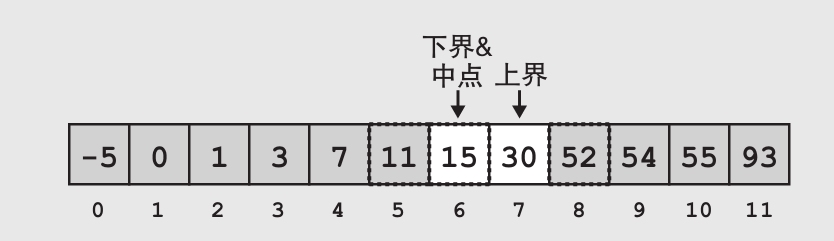
请注意，通过这几次的操作，此时虽然下界已经是目标值了（v=15），但是我们仍需要继续搜索，直到中间值指向目标值。这是因为二分搜索是对中间值进行判定，而不会判定上界和下界是否是目标值。

如果目标值不在数组中会发生什么呢？在搜索过程中，上下界之间的距离会越来越近，直到它们之间没有任何还未检查过的值。因为我们总是将其中一个界限移动到中间值的另一边，所以我们可以在IndexHigh<Indexlow的时候停下来，这个时候就可以保证目标值不在数组中了。