10 用广度优先搜索去开锁（第2/3页）

门上的“确认”按钮短暂地闪了一下，紧接着发出了一声短暂的咔嚓声。不过门依然是锁着的。咒语刚刚尝试了第一个可能的密码——空密码。紧接着，泥泞的地上出现了一列字母和数字：

1，2，3，A，B，C

Frank在头脑中想象了一下这个选项列表所对应的搜索树：

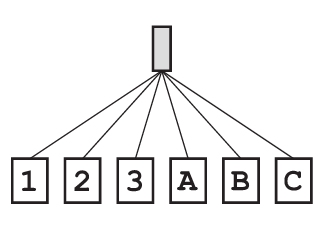
数字1随即亮了起来，随后“确认”按钮也亮了起来。再一次，门发出了咔嚓一声，但依然是锁住的。地上的列表再一次变了，这次加入了搜索树第三层的一些可能的密码：

2，3，A，B，C

11，12，13，1A，1B，1C

但这些新的可能的密码被加到了列表的最后，而搜索算法本身依然还在继续尝试第二层剩下的密码。

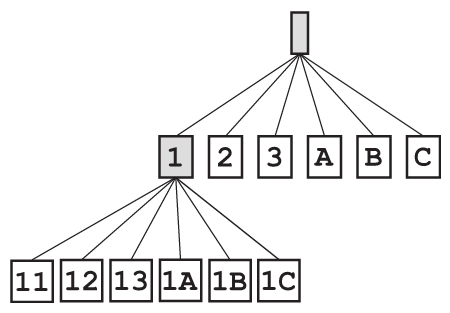
密码2也不对，列表再一次变长了：

3，A，B，C

11，12，13，1A，1B，1C

21，22，23，2A，2B，2C

再一次，搜索树的最后一层延伸出了新的可能性。但搜索算法本身依然停留在第二层继续尝试，在尝试完所有一位的密码后才会进入到搜索树的下一层。

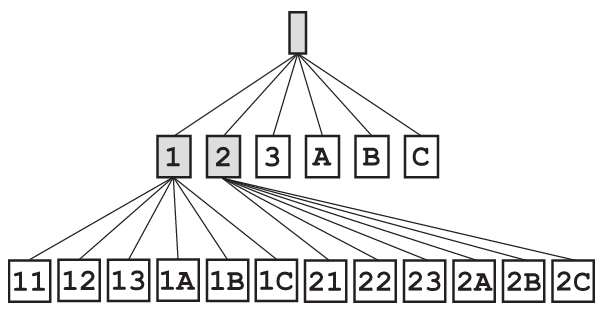
换句话说，搜索算法在尝试完当前层的所有可能密码后，才会进入下一层。

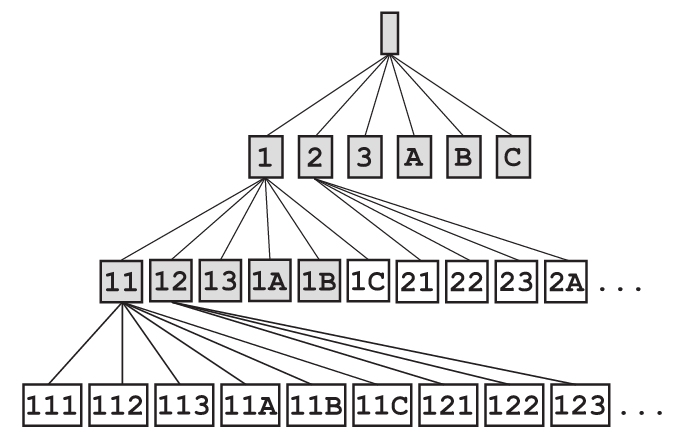
搜索算法又尝试了3、A、B、C这四个可能性，完成了整个搜索树的第二层的尝试。Socks这时说道：“这估计得花上一段时间了。”

Frank点了点头，眼睛一动不动地盯着地上不断变长的数字列表。“Notation，不如你去前面侦查一下吧？”

“好的，”她同意道，眼神中透出明显的解脱。新手警察一般都不善于长时间地等待，毕竟警察学院也没有办法教你如何一动不动地坐上几个小时。不过话说回来，听学院里Cloud教授的执法课其实也跟干坐着差不多无聊了。

Notation走后五分钟，锁发出了一声响亮的咔嚓声。随后，锈迹斑斑的大门随着巨大的噪声慢慢地打开了。随着搜索算法顺利完成，地上写着的列表也渐渐消失掉了。

“1111。”Frank说道，他看起来一点都不惊讶。毕竟密码必须设得足够简单，那些小喽啰们才能记住。

他用棍子把密码写在了地上的一块泥土上，又围着它画了两个圈。再怎么新手的警察也应该能看得出来这是留给她的消息。接着，他转向Socks，说道：“我们走吧。”

警用算法导论：广度优先搜索

节选自Drecker教授讲义

广度优先搜索是一个按顺序依次尝试可能的搜索选项的算法。换句话说，它每次都会选择尝试最先发现的但还没有尝试过的选项。

你可以想象一个列表（更具体地说，是一个队列），上面存着所有已知的但还没有尝试过的状态（选项）。每一步，算法都会选择从当前队列的第一个状态开始进行尝试。当发现新的可能性时，就将其加到队列的最后，以确保算法在尝试完所有先前已经发现的可能状态后才会去尝试这个新发现的状态。

让我们想象一下广度优先搜索算法是怎么搜索一个图的。一个图是一种由点和边组成的数据结构。如果两个点由一条边相连，我们就可以说这两个点是相邻的。在警用算法课上你已经见识到了一个图：Kingdom HighwayMap。这个图里的每个点代表一个城市，而每条边则代表一条连接两个城市的高速公路。罪犯们一般都倾向于逃离他们所在城市，而你则需要找出他们最可能逃到哪些相邻的城市。

搜索Kingdom HighwayMap是一个经典的图上搜索问题。我们搜索的状态是图上的点，也就是地图上的城市。假设现在有人在A城市犯了罪，而你的目标是找到罪犯在哪。

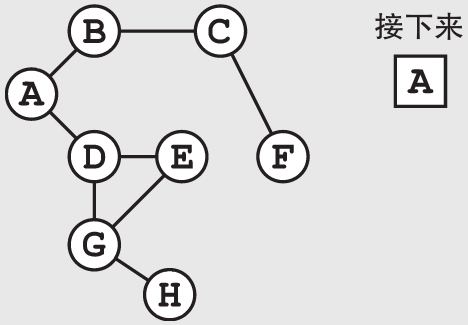
广度优先搜索会沿着一个不断延伸的边界展开。这个算法会先检查所有离起点X步的点，然后才会继续检查离起点X+1步的点。当你检查完A城市后，它的两个相邻城市B和D会被加到队列的最后。此时的队列中没有别的城市了，所以接下来算法会检查B城市。

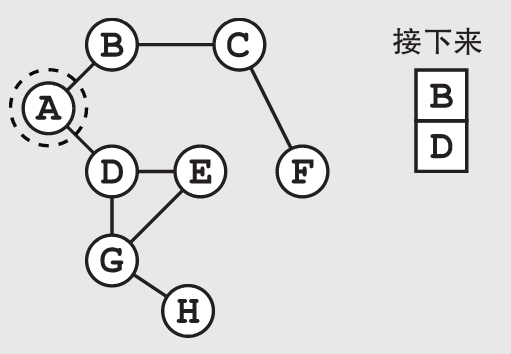
如果每个点都有很多相邻的点的话，维护这个队列就会占用大量的内存空间。在搜索一个大规模的问题时，这个内存需求会变得相当巨大。这时，作为警官的你就会打算多买一些质量好的笔记本。

在广度优先搜索的每一步，我们都需要先看看当前的点是不是我们的最终目标。在这个具体的例子当中，我们需要把当前点对应的城市仔细搜查一遍，看看罪犯是不是藏在这个城市中。如果当前的点还不是我们想找的目标，就把与它相邻的点中还未被检查过的点（也就是我们之前从来没有加到列表中的点）加到列表中。如此一来，我们可以避免重复添加已经检查过的点，以及虽然还未检查过但已经在列表里的点。在这个具体的例子中，检查过城市B后，我们将不会重复添加城市A（虽然它和B城市是相邻的，但我们已经检查过它了）。

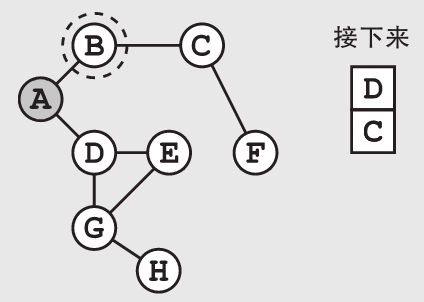
请注意，如果我们想要检查一个点在之前是否已经被添加过，将需要更多的内存，因为我们需要记录下所有已经被加入过列表中的点。不过这样做会给我们带来巨大的好处——可以避免重复多次检查同一个点。重申一遍，仔细地记录下已经检查过的点会给你带来巨大的好处。

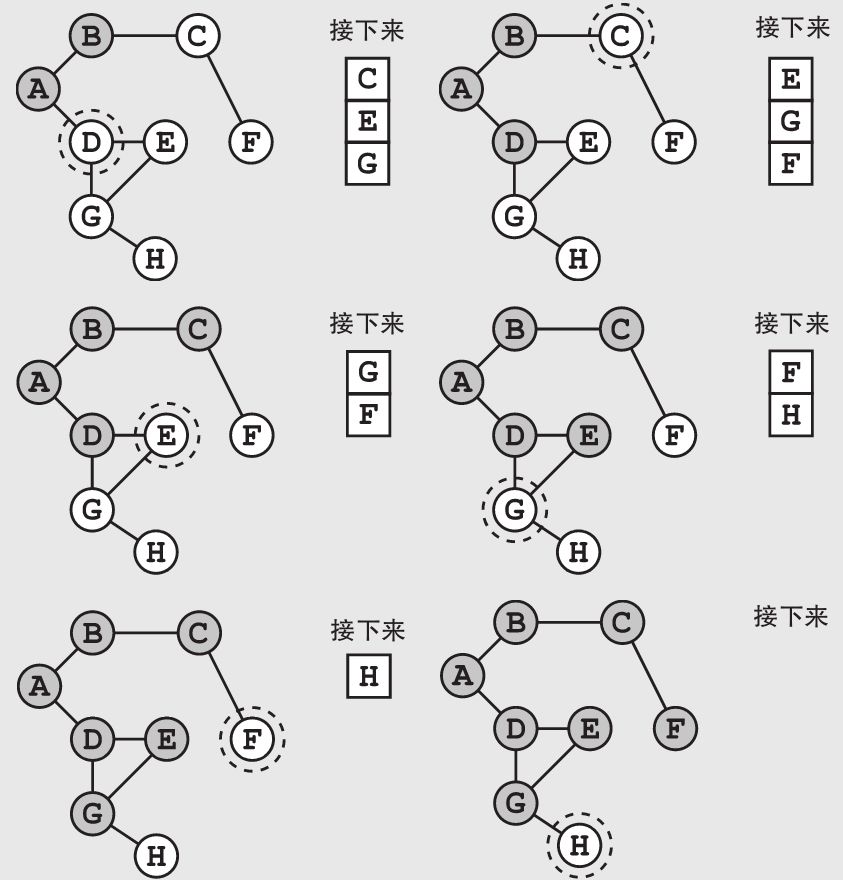
在这个具体的例子中，我们在H城市找到了要找的罪犯。至此我们可以在H城市逮捕他，结束搜索。

在搜索问题中，如果任意相邻的两个点之间移动的代价（例如所需的时间、体力，等等）是相等的，那么广度优先搜索可以保证找到一条花费最小代价的路径。这是因为它在检查完所有离起点距离X步的点后，才会开始检查那些更远的，例如离起点距离X+1步的点。

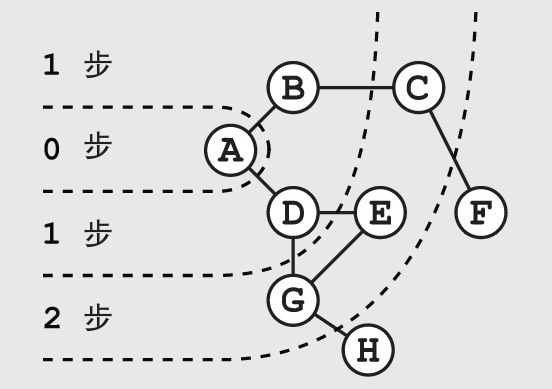
如果对于每个点都记下它是由哪一个点走来的，我们就可以很容易地追溯到这条最短路径。我们只要从终点开始，不断地回溯到它之前的一个点，直到回到起点就好了。

不过，值得注意的是，广度优先搜索只有在相邻点之间移动的代价都一样时才会给出最优的方案。一般来说，找出两点之间步数最少的路径和找出两点之间代价最小的路径是不一样的。举个例子，如果一群远足者想要尽量节省体力的话，他们宁愿会走一条相对较长但可以避开山路的路，即使穿山而过可能会使整个路程更短，也会更有观光价值，但走这段山路无疑会耗费更多的体力。