19 疑犯的二叉搜索树（第2/2页）

“对于右子树也是同样的道理。如果当前点的值比我们要找的区间中的最大值还大的话，我们就可以跳过右子树。否则，就需要继续向右子树里面搜索。

“现在我们要找的区间是50到70。对于这个节点55，由于其左子树中的值最大可能是55，所以其中的点可能会落在我们要找的区间中，所以我们需要去探索左子树。右子树里面的值可能会大于55，这也和我们要找的区间有重叠，所以我们也需要探索右子树。我们先从左子树开始。

“现在的节点上显示的是22天，”Frank继续说道，“我们不需要将它放进结果列表。并且，因为所有在它左子树里面的值都会比22小，因此我们也不需要去检查它的左子树了。”

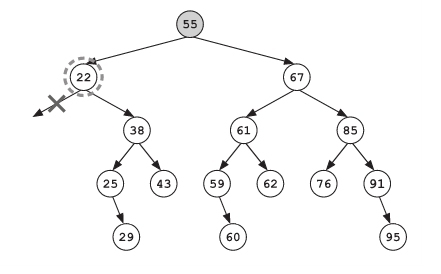
“我们把这种情况叫作搜索中的剪枝，”Notation补充道，“因为这就像从一棵树上面砍下了一个分支一样。”

当Frank看向她的时候，她想起来她不应该和Frank说话，便又沉默了。

“所以我们只要探索右边的分支就好。”Frank说道。

“递归着探索！”Socks补充道，听起来他简直太欢乐了。

“对，递归着探索，”Frank冷淡地同意道，“现在的节点上是38天。同样的，我们不需要将它加到结果列表中，并且我们也可以跳过它的左子树。”

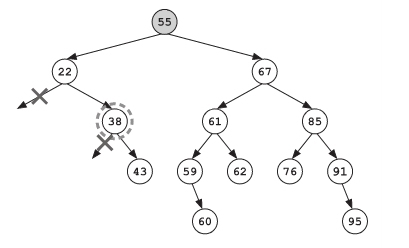
“但我们需要递归探索它的右子树。”Socks说道。看起来他挺享受这个新的算法。

Frank点了点头。

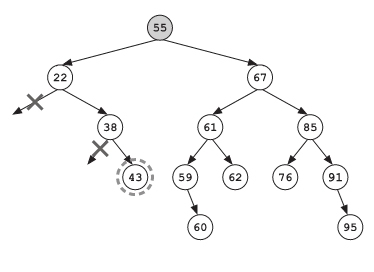
下一个点没有子节点了。它已经是一条死路了。

“现在呢？”Socks问道。

“和深度优先搜索一样，”Frank说道，“我们倒退，并且选择之前还没有探索过的路线，直到我们将整棵树都搜索过了为止。因为我们一路上剪掉了很多分支，所以我们需要一直倒退到根节点。”

搜索接着在根节点的右子树里开始了。被找到的新记录被加入了结果列表，不合适的分支被一个个剪掉，而合适的分支则被递归地探索着。

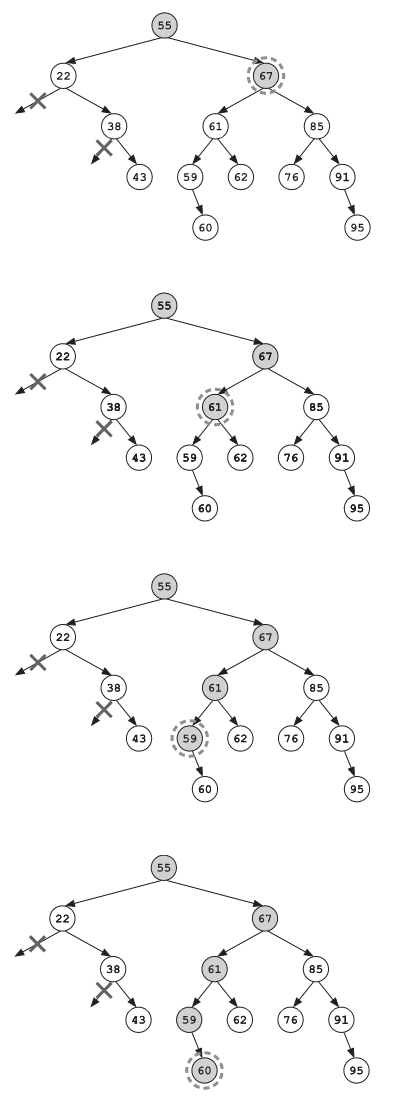
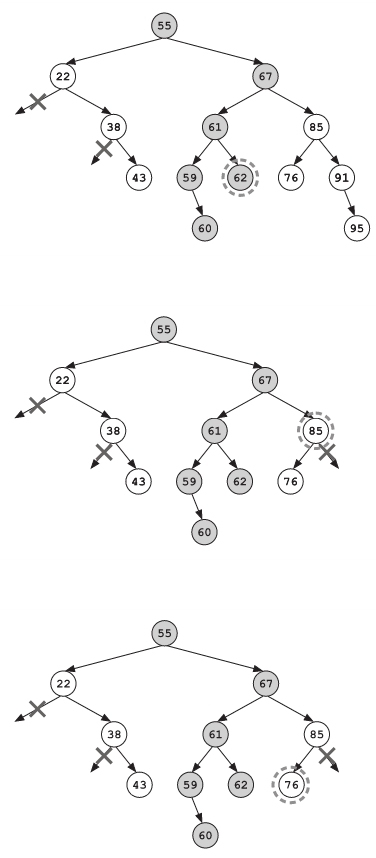
最后他们找到了几条符合条件的调职记录。Frank仔细地研究了找到的结果，试图找出任何可疑的地方。

“什么都没有，”他难以置信地低吼了一声，“这里面什么都没有！”

警用算法导论：二叉搜索树Ⅲ

节选自Drecker教授讲义

在二叉搜索树上进行区间查找和查找一个元素类似。算法从最顶端的根节点开始，一路递归着搜索整棵树。它根据以下三个条件来对在每一个节点做决定：

1.当前节点应该被算在结果中吗？如果当前节点在要找的区间内，我们就应该将它加到结果列表中。

2.应该探索左子树吗？如果当前节点有左子树，并且当前节点的值大于区间里最小值，我们就应该递归探索它的左子树。因为这种情况下，它的左子树可能包括区间内的值。

3.应该探索右子树吗？如果当前节点有右子树，并且当前节点的值小于区间里最大值，我们就应该递归探索它的右子树。因为这种情况下，它的右子树可能包括区间内的值。

使用二叉搜索树来做区间搜索的优势在于，可以通过剪去大量不可能包含要找的值的分支来减少计算量。

考虑如下的二叉搜索树：

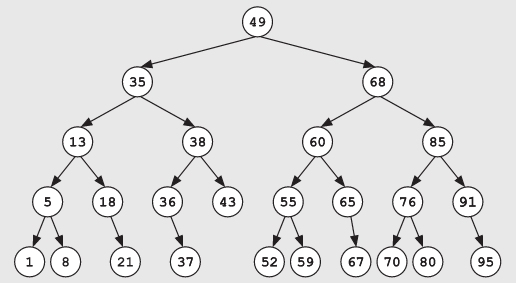
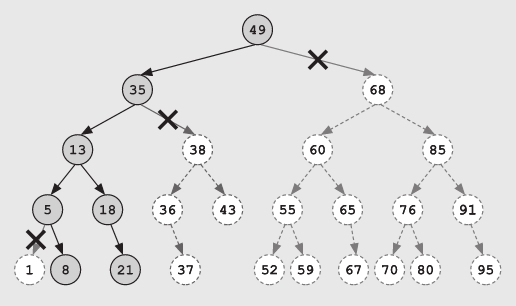
如果想找在区间[8，20]内的所有值，你只需要访问全部25个节点中的7个（被访问的节点被标上了阴影）：

类似的，如果想找在区间[70，80]内的所有值，你只需要访问全部25个节点中的6个：

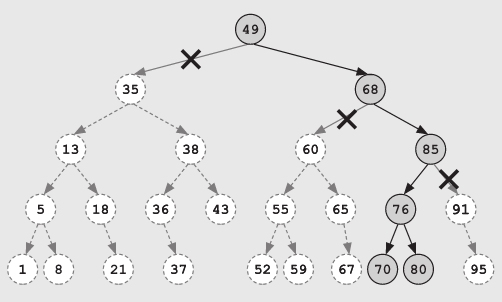
需要注意的是，访问一个节点不一定代表这个节点会被包括在最终结果列表里。在我们给出的两个例子中，可以看到算法也需要访问一些不在目标范围内的节点。之所以访问它们，是因为那些节点的子树可能包括我们想找的值。

和寻找一个值一样，用二叉搜索树做区间搜索只有在需要进行多次搜索时才高效。建立一棵二叉搜索树比搜索一遍数据需要更大的计算量。但是如果要搜索多次，这个计算量可以被均摊到多次搜索里，从而让每次搜索的平均计算量变小。

1. 1 剪枝，这是一个很形象的说法。在搜索算法优化中，就是通过某种判断，避免一些不必要的遍历过程。简单是说就是不用去遍历每个节点，形象点说就是剪去了搜索树中的某些肯定不需要考虑的“枝条”，故称剪枝。——译者注返回