23 最佳优先搜索：侦探最值得信赖的工具（第2/3页）

这句话意味着现在的情形非常严重。Ann公主几乎永远都在出使任务、调查或者是谈判。既然她回来了，那现在的情况一定糟糕透了。

“Ann公主正在回来的路上？”Frank问。

“她认为最近的袭击一定和Unnecessary Complexity联盟有关。”

“Unnecessary Complexity联盟？”

“一切都和那个叫Exponentious的邪恶巫师有关，”警长说，“就是那个总是想摧毁王国的巫师。”

Frank点了点头。很显然，他还清楚地记得当年Exponentious发动的袭击所带来的恐慌。在那些天里，关于他发起的这次运动一直在年轻巫师与骑士中间流传。

警长继续说道：“他现在被牢牢地关在皇家监狱里，但Ann公主担心他可能有别的团伙在行动。比如说他的追随者、帮凶或者崇拜他的人。Ann公主一直在找有关这个神秘巫师联盟的线索，目前他们一直躲在阴暗处，进行一些小范围的袭击，但是皇室成员非常担心。”

Frank一脸茫然地盯着警长。这会不会就是Vinettee提到的那个联盟？如果真是的话，那么他怎么会把自己牵扯到这种事情中来。于是Frank脑中又萌生出了另一种假设。

“攻击城堡！会不会和Ann公主返回有关？”Frank说，“如果她在调查Unnecessary Complexity联盟，他们有可能会报复她。”

“我们已经想到了这一点，”警长说，“当Ann公主回来时，我会调派一百多个警察去保护她。虽然这会使军械库、监狱和警局的警力减少，但我们绝不能让Ann公主有任何闪失。”

“那魔法面具呢？有人会利用面具潜入安保人员的队伍。”

“是的，这是一个溜进城堡的绝好机会，”警长承认道，“即使没戴面具，在增加了一百多个新的警察后，我们也很难在人群中找出他们。但是我们采取了措施，皇家巫师Marcus创造了一种有魔法的身份徽章分配给那些城堡的安保人员。身份徽章是无法伪造的，一旦佩戴的人与徽章上的照片或者名字不一样，徽章就会发出红色的光。”

Frank努力思考是否还有其他的安全隐患。

“你再想想，”警长说，“你还有没有发现别的问题？”

Frank飞速地思考着，回忆他们在TCP Flyer号船上发生的事，以及他们在Mudwall和Frayed Cable岛上的搜索。他描述了监狱中遇到的袭击和公文被烧毁的经过，最终，他从调职记录中找到了更多线索。

“这也是为什么你想了解Notation的原因吧，”警长说，“她是刚从警察学院调过来的。”

“确实，”Frank承认，“她的名字在我的搜索范围之内。”

警长想了想后说道：“我不认为她是这种人，我的直觉告诉我，她是一个好警官，但是我不确定我现在应该相信谁。不管怎样她是不应该去调查这个案子的，这并不是她的任务。”

“谢谢你。”Frank说道。

“还有没有其他新调来的人需要去特别关注的？”

Frank摇摇头：“新调来的警察们分布在不同的犯罪现场，但是没有规律，没有任何一人与两个以上的盗窃案相关，除非一整个班都是叛徒才有可能，所以我认为这行不通。”

“你调查得很好，Frank。”警长说道，“这是我这么多年来见过的能把最佳优先搜索用到极致的案例之一。”

Frank笑了，即使在警队，也很少有人会知道这种类型的调查需要使用最佳优先搜索。多数人只会说“我正在调查”或是“这些线索我正在跟进”。

尽管对其认知不足，最佳优先搜索仍是警官们办案必备法宝之一，它就像记事本或者是一双舒服的鞋子一样重要。在最佳优先搜索中，你需要时刻维护一个线索列表，每次从中选择最可靠的一个线索去调查，调查完毕后，再从列表中选出下一个最可靠的线索继续调查。当然如果在调查的过程中发现了新的线索，就将其及时加入到列表中。这种方法对于查案很有帮助。

Frank摇摇头。

“那好，”警长说，“继续调查。如果Unnecessary Complexity联盟真的存在，而且一直在背后操纵这个案子，那么我们已经深陷危机之中了。注意安全，Frank。”

“我一向很谨慎。”Frank回答，他站了起来，又停住了，“最后一个问题，你知道Notation是如何知道Array Cart的吗？”

“我不知道，”警长回答道，“为什么不直接问问她呢，她现在似乎正站在我的办公室门口。”

警用算法导论：最佳优先搜索

节选自Drecker教授讲义

假如你在这门课程中只记住了一个算法，那么你一定要记住最佳优先搜索这个算法，它将是你警队生涯中最有用的工具。也许所有的案件到最后你都需要使用这个算法。

最佳优先搜索是基于某种估值分数或者评价函数来选择接下来探索哪个状态的算法。每一个新发现的状态也都将被赋予一个分数，这个分数就是算法对这个新发现状态的估值。例如，我们可以为每一个状态标记上一个值，可能是目标状态的概率（如果这个概率可以被估计的话）或者是在调查中线索的重要程度。其实最佳优先搜索就是在每时每刻维护着一个带有估值分数的状态列表，每次从这个有序列表取出下一个估值分数最高的状态去探索。

当然，最佳优先搜索也可以按照代价最小的规则来选取下一个要探索的状态，这个代价可以是当前状态到目标状态的估算距离。在这种情况下，每一步都要选择列表中估值最小的一个状态进行探索。

我们来看一个迷宫问题。现在我们已知起点和终点的坐标，可以在搜索空间中为每个点（状态）都设置一个值，这个值就可以是从该点到终点的距离，例如，可以使用曼哈顿距离——两点之间的垂直距离加上水平距离之和。虽然这个值不一定意味着当前点到目标点的实际步数，但它可以为最佳优先搜索算法提供更有效的选择依据。

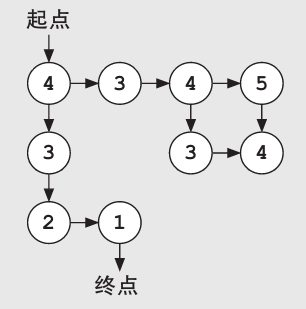
随着搜索的进行，算法开始尝试探索不同的点（即下图中带阴影的圆圈），每当遇到一个新点，都要将其添加到一个列表中等待之后进一步探索（即下图中带有虚线的圆圈）。在每次迭代中，算法将根据每个点的估值分数来选择最佳的那个点去探索。在这个例子中，每次将选择估值最小的那个点去探索。

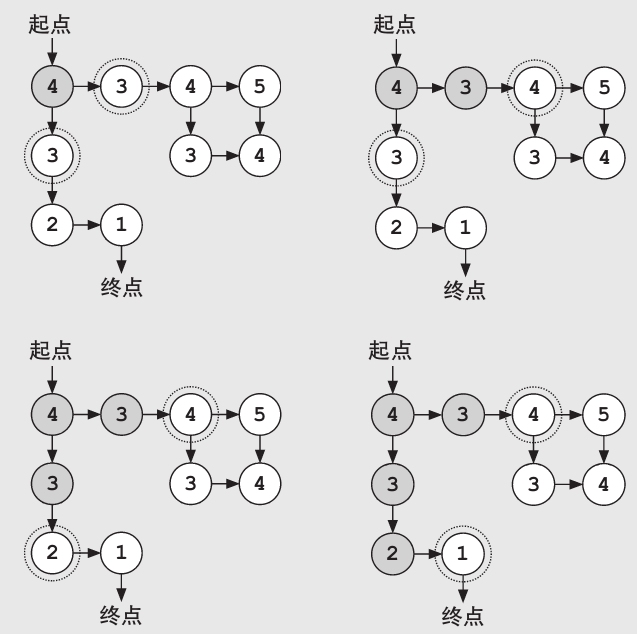
一旦找到目标点，我们就可以终止搜索。在这个例子中，我们只需要探索一半多一点的点。例如，我们不会选择探索第二个距离为4的点，因为我们总是有一个更好的选择可以优先尝试。