27 警察学院中的“堆”（第2/2页）

“你到底为什么需要这个信息？”她问。

“我在调查首都警局的盗窃案。”他回答道，心里想：她先是胡言乱语地说了一通故事，现在居然又要盘问我？我时间可不多了。

“我需要看你的警徽。”Loop教授伸出手来。

Frank从他的披风口袋里找出私人侦探的徽章，扔在她的桌上。

“私人侦探？”Loop教授笑了笑，然后她的声音又变得非常强硬，“给我出去。”

“Loop教授……”Frank的声音被插销的上锁声打断。

警用算法导论：堆

节选自Drecker教授讲义

最大堆是基于二叉搜索树的数据结构，它的每个节点与其子节点之间需要时刻维持有序关系。具体来说，堆在存储元素时一定要遵循堆的特性，对于最大堆，树中的任意一个节点的值都要大于（或等于）其下面的所有节点。这种结构允许最大堆高效地支持几个非常重要的操作：（1）找到最大的元素，（2）删除最大的元素，（3）插入任意元素。这三个操作使得堆成为实现优先级队列的理想数据结构。

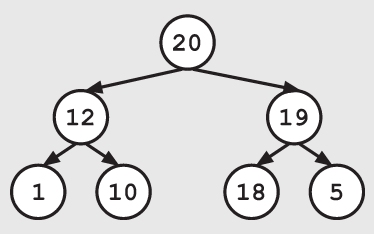
堆看起来像一棵树，它很容易通过数组来实现，其中数组中的每个元素对应了树中的一个节点，根节点位于索引0处，如下页图所示。子节点索引可以通过父节点的索引计算得到。具体来说就是，索引i处节点的子节点位于索引2×i+1和2×i+2处。因此，索引1处节点的两个子节点分别位于索引（2×1）+1=3和索引（2×1）+2=4处，如下页图所示。

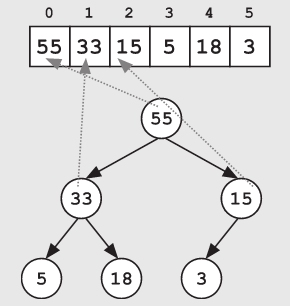
有时为了简单起见，一些堆在实现的时候直接跳过了数组索引0。根节点被放置在索引1处。在这种情况下，索引i处节点的子节点位于索引2×i和2×i+1处，这使得索引计算更为简单。无论哪种方式，都可以便捷地通过父节点的索引值来计算出两个子节点的索引值，也可以通过子节点的索引值计算出父节点的索引值（子节点的索引值除以2后向下取整便可得到其父节点的索引值）。

由于根节点（数组中的第一个元素）总是最大堆中的最大值，因此你可以始终在固定时间内获取该值，而不论数组中还有多少其他元素。这使得用户可以有效地查找优先级队列中的最高值元素。

如果你想添加一个元素或删除最大元素，这个过程会更复杂，需要首先打破堆的特性，然后再逐步恢复堆的特性。

为了添加一个新元素，首先将新的元素添加到数组的最后面（即树底层中的第一个空白处）。如果新添加入节点的值大于其父节点的值，这将破坏堆特性，因此需要将此节点向上移动，直到它不再大于其父节点的值，并重新恢复堆的特性。也就是说，如果新加入节点的值大于其父节点的值，就不断地将该节点的值与其父节点的值进行交换。例如，如果要将60这个数添加到前面的堆中，则首先将它插入底部，然后将其向上移动，进行两次与上一级节点的交换操作。因为第一次在与15交换后，该节点的值仍然大于其新的父节点55，所以还需要再与55交换一次。

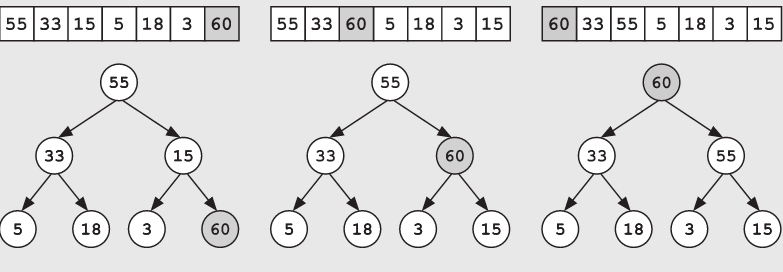
删除最大值元素也是类似的。将原来的最大值与数组的最后一个元素交换位置，使原来最后的那个元素成为新的根节点。

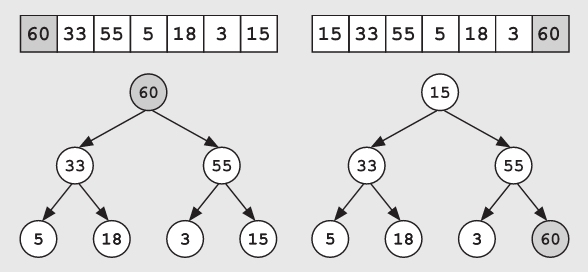
接下来删除现在最后的这个元素就可以了（此时原来的最大值已经成为数组的最后一个元素）。虽然现在已经正确地删除了原来的最大值的节点，但这个操作也破坏了堆的特性。

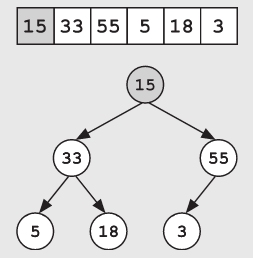
我们需要从新的根节点开始沿树向下调整该节点，以恢复堆的特性。在树的每一层，我们将该节点的值与其子节点进行比较。如果该值小于它的任何一个子节点的值，就需要将该值向下移动，并将两个子节点中值较大的那个子节点与其交换位置，以恢复堆的特性。直到该节点的子节点都比这个值小时，就结束操作。

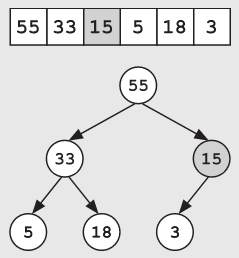
插入新元素和删除最大元素的操作都需要我们从树顶部逐层调整直至合适的位置，不过最多只需从顶部到底部调整一遍。如果要往堆中增加一倍的节点，只需要在堆的底部增加一层节点即可，所以此时的插入和删除操作依然很快，即使是一个大的堆也会很快。换句话说，虽然堆的节点总数增加了一倍，但堆的层数只增加了一层，插入和删除操作仅比原来多交换一次。此外，由于上述插入和删除操作可以保持树的平衡，所以之后的操作也同样是高效的。